1. With the help of a diagram, explain how it is possible for a firm in perfect competition to earn abnormal profits in the short-run.
The short-run is the fixed plant period, or the period in which firms cannot enter or exit an industry. Firms in a perfectly competitive (PC) market are price-takers, meaning that they must accept the market price. In the short-run, the firm is maximizing profits by producing at quantity q, where marginal costs equal marginal revenue (MC = MR). This maximizes profits because the last unit produced brings more additional revenue (MR) than the additional cost (MC) it causes. The cost per unit (average cost) is C and the revenue per unit (average revenue) is P. This means that the average cost is less than the average revenue and the firm is making abnormal profit (P-C) on each unit. The shaded area shows the abnormal profit per unit. Abnormal profits are when the firm’s revenues exceed all costs and normal profit. Where abnormal profits are earned, firms are attracted to join the industry. However, the short-run is the fixed plant period, where no firms can enter the industry, so there will be no change in the industries supply curve which could cause a decrease in price for a firm. This is why earning abnormal (or economic) profits is only possible in the short-run.
2. With the help of a diagram, explain how it is impossible for a firm in perfect competition to earn abnormal profits in the long-run.
Since there is perfect knowledge of the industry, firms will enter the industry because they seek to earn abnormal profits. When more firms enter the industry, the industry supply curve will shift to the right. The industry price falls from P to P1. Because the firms are price-takers, the price falls and the demand curve for a firm in the industry shifts downwards. The firms are now making normal profits with the price per unit equal to the cost per unit.
In the long-run a firm can't earn abnormal profits, because abnormal profits attract firms to enter the industry, and in the long-run these will cause the industries supply curve to shift to the right, causing a firm’s price to decrease, erasing the abnormal profits that were earned in the short-run.
3. Explain whether or not a firm in perfect competition earning abnormal profits is productively and allocatively efficient.
A firm is said to be productively efficient if it is using its resources to their maximum efficiency by producing their output at the lowest possible average total cost (P = minimum ATC).
A firm earning abnormal profits is not productively efficient because firms are constantly trying to maximize profits which is why a firm would produce at quantity Q, where P = MC. In order for the firm to be productively efficient its quantity produced would have to decrease from Q to Q1, which is the point where P = minimum ATC).
Allocative efficiency i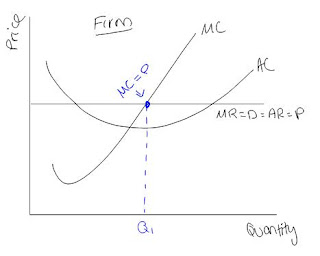
A firm earning abnormal profits is productively efficient because it produces at Q1, where P = MC. At this point the firm is maximizing profits and is producing allocatively efficient.
Therefore, a firm in a perfectly competitive market earning abnormal profits is never productively efficient, while it is always producing at allocative efficiency.




#1: Perfect answer.
ReplyDelete#2: Very good.
#3: Oops. You say "a firm earning abnormal profits is productively efficient..." I think this is a mistake. But you recover in the last sentence. Well done!
You get an A! Happy Holidays!